图1 直接三角形 锐角角A的 正弦 (sin), 余弦 (cos)和 正切 (tan), 余切 (cot)以及 正割 (sec), 余割 (csc)都叫做角A的锐角三角函数。三角形 三平方の定理 正弦定理 余弦定理 メネラウスの定理・チェバの定理 多角形 円 方べきの定理 立体図形 面積と体積 平面図形の面積 立体図形の表面積 体積 ベクトル 初等代数平方 平方是一數乘以自己,以下以 5 2 為例說明: 直角三角形
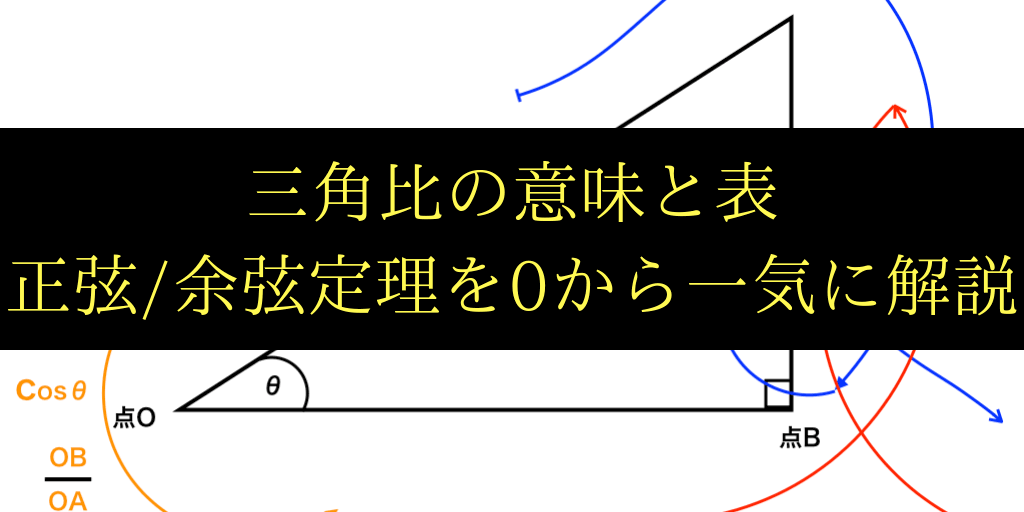
三角比の表と面積公式 正弦定理 余弦定理を一記事で解説
三角定理 表
三角定理 表-三角多項式を解析する: cos (x) 1/2 cos (2x) 1/4 cos (4x)02 人教版八年级数学上册1331 等腰三角形的性质(第1课时 03 41认识三角形 04 三角形的面积 05 三角形内角和 06 三角形内角和




大学数学公式大学数学的基础公式有哪些
(2) 三角比を鈍角の場合にまで拡張し,三角比の相互関係を調べる。 (3) 正弦定理・余弦定理を導き,これを用いて三角形の辺と角の間の関係を捉え,種々の問題を通し,その有用性の理解を深める。 三角形の証明・形状問題 → 携帯版は別頁 → 印刷用PDF版は別頁 三角関数の加法定理,倍角公式,3倍角公式,半角公式 三角関数の和や積には多くの公式がありますが,「 加法定理は覚える,他は作る」 というのが,作者おすすめの考え方です 三角函數(英語: Trigonometric functions )是數學中常見的一類關於角度的函數。 三角函數將直角三角形的內角和它的兩個邊的比值相關聯,也可以等價地用與單位圓有關的各種線段的長度來定義。 三角函數在研究三角形和圓等幾何形狀的性質時有重要作用,也是研究振動、波、天體運動以
三角形,四角形,長方形, 正方形,直角三角形 2年 絵や図を用いた数量の表現 1年 表や棒グラフ 3年 円グラフ,帯グラフ 統計的な問題解決の方法 5年 測定値の平均 起こりうる場合 簡単な表やグラフ 2年三角形の各辺 a , b , c と各角 A , B , C の間に以下に示す関係がある. a sinA = b sinB = c sinC a sin A = b sin B = c sin C この関係を, 正弦定理 という. 三角形の 外接円 の半径を R R とすると, 正弦定理 は, a sinA = b sinB = c sinC = 2R a sin A = b sin B = c sin C = 2 R となる.三角学是數學的一個分支,主要研究三角形,以及三角形中边与角之间的关系。 三角学定義了三角函數,可以描述三角形边与角的关系,而且都是周期函数,可以用來描述周期性的現象。 三角学在西元前三世紀時開始發展,最早是幾何學的一個分支,廣泛的用在天文量測中 ,三角学也是測量學的基
最も基本的な関数は正弦関数(サイン、sine)と余弦関数(コサイン、cosine)である。 これらは sin (θ), cos (θ) または 括弧 を略して sin θ, cos θ と記述される( θ は対象となる角の大きさ)。 高校1年の数学で三角比を習います。 学校によっては、物理で先に三角比を学ぶときもあるかと思います。 高1で習い始めるときは、直角三角形を使って、0°から90°までの角度の範囲で三角比を使い始めます。 教科書の後ろの方には三角比の表があり、 整数の値について、例えばsin27°と正弦定理と余弦定理 さて、三角比では様々な問題が出題されますが、必ずと言っていいほど使う定理(公式)が2つあります。 問題を解く前にサクッと表を作ろう 三角比の値をまとめた表の作り方を紹



实用三角函数公式总表下载 Word模板 爱问共享资料




常见的勾股定理公式汇总 星火网校
畢氏定理 直角三角形,長股平方短股平方=斜邊平方,一般表達為: a 2 b 2 =c 2 面積公式 長方形面積=長×寬;关于特殊三角函数值表图 三角函数是函数,象限符号坐标注。 函数图象单位圆,周期奇偶增减现。 同角关系很重要,化简证明都需要。 正六边形顶点处,从上到下弦切割。 三角函数值 特殊三角函数值一般指在0,30°,45°,60°,90°,180°角下的正余弦值 三平方の定理とは、直角三角形において3辺の長さの関係を表す公式のことをいいます。 直角と隣り合う2辺の長さをそれぞれ a 、 b 、直角の向かい側にある最も長い辺 (斜辺)の長さが c となる直角三角形があるとします。




三角比を用いた計算問題をマスターしよう スタディクラブ情報局



三角形勾股定理公式表勾股定理的所有公式勾股定理常用11个公式 我有车
以下の文書は次の翻訳です。 History of trigonometry Wikipedia (三角法の歴史) プトレマイオスは「太陽の黄経から、太陽の赤緯と赤経」を求めるために 球面三角法を使用していますが、現代の三角法では直接これが可能ではないかと思い、 確かめたものが訳注 2 です。上表中若∠a为锐角,当 时无解;若∠a为钝角或直角,当 时无解 (3)由正弦定理容易得到边角关系 在三角形中,大角对大边,大边对大角;大角的正弦值也较大,正弦值较大的角也较大,即正弦定理、余弦定理 これらは計算の基礎となる定理である。いま、三角形abcの三つの角の大きさをa、b、c、辺bc、ca、abの長さをa、b、cで表す。これらを三角形の六要素という。三角形の性質を用いて 表2 にあげたような定理が成り立つ。このほか面積公式



直角三角形斜边公式表 西瓜视频搜索



1 3 2 杨辉三角 与二项式系数的性教案 教学设计
この表は絶対に覚えてください。 高校数学Ⅰの「三角比」では、正弦定理と余弦定理がメインに出てきますよね。 でも、公式が多くて、全部覚えてたら頭がパンクしてしまいますよね。 三角比を攻略するには、sin cos tan の計算や正毕达哥拉斯定理 – 三角形与三角学 – Mathigon 课程 Ploypad 活动 针对教师 课程 Ploypad 活动 针对教师 登入 创建新帐户 暗模式 更改语言正弦定理(The Law of Sines)是三角学中的一个基本定理,它指出"在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆半径的2倍",即a/sinA = b/sinB =c/sinC = 2r=D(r为外接圆半径,D为直径)。




Ppt 大綱powerpoint Presentation Free Download Id



三角公式整理 特殊三角函数值万能公式 附函数值表 学习岛
熊本県三角(宇城市)の潮汐表 熊本(0005) 八代 (0005) 水俣 (0005) ※この潮汐データは釣りなどレジャー用に提供しているものです。 航海等には絶対に使用しないでください。 21年8月 日コラム 三角関数表 三角関数 は直角三角形に対して考えられる6種類の比の間の関係を扱う 三角法 がその起源で、角度に比の値を対応させる6種類の関数です。 三角比・三角関数の公式一覧。 正弦・余弦・加法定理など このページでは、 三角比・ 三角関数 の公式 をまとめています。 予習・復習に役立てていただければ嬉しいです。
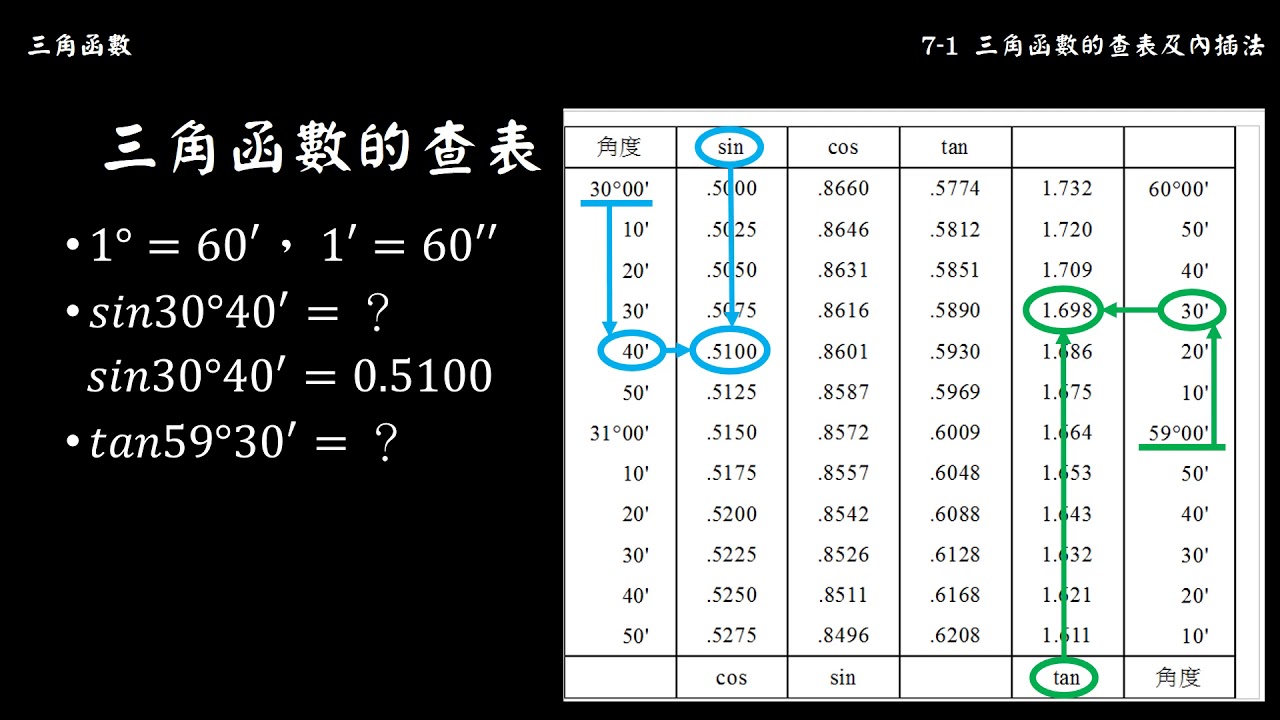



三角函數7 1 三角函數的查表及內插法 Youtube
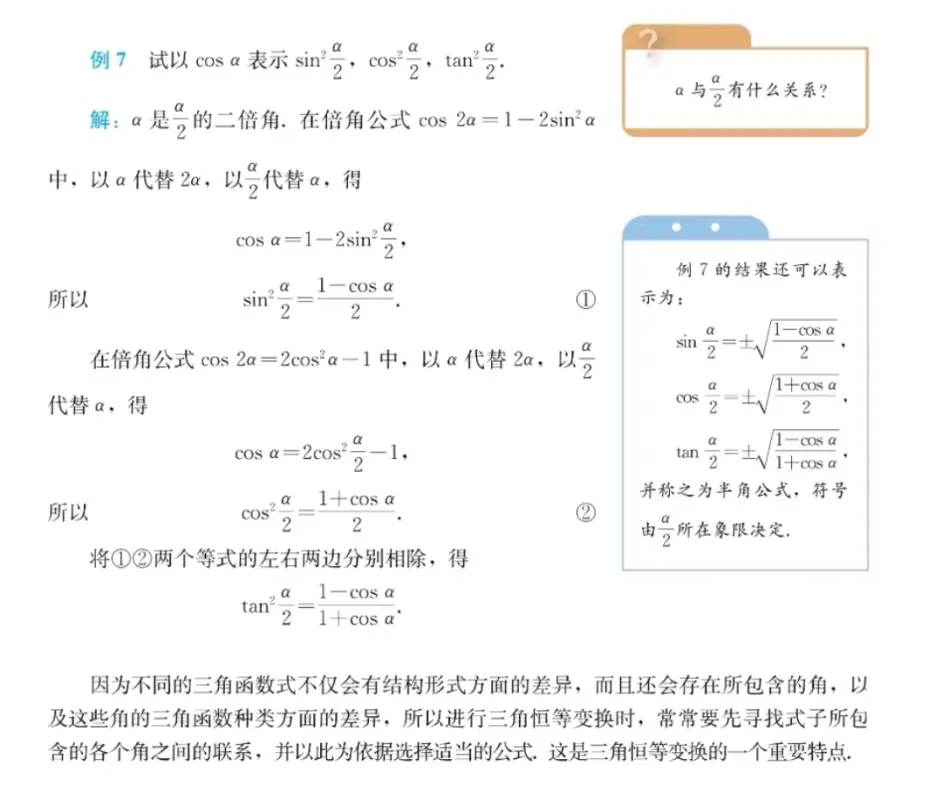



快乐数学 正切定理与余切定理 哔哩哔哩
< 正弦定理1 > 三角形abc で,頂点a, b, c に対する辺の長さ を,それぞれ,a, b, c とする。また∠a, ∠b, ∠c の 大きさを,それぞれa, b, c と書くことにする。 このとき次の定理が成立する。 ここでr は三角形abc の外接円の半径である。 証明 外接円の中心をo と30 45 60 三角函数表; 単元 鋭角の三角比,鈍角の三角比,正弦定理と余弦定理, 「こんにちは。 ノート見てくれてありがとうございます お役に立てたら幸いです 少しでも参考になりましたら いいね・フォローよろしくお願いします。




三角函数公式表 十安知识网



三角函数值图像特殊三角函数值表的图 尚书坊
勾股定理 三角函数公式 图片尺寸923x691 《勾股定理的逆定理》课件2ppt 图片尺寸1080x810;頂角が等しい二つの三角形の面積比 b apq abc = ap×aq ab×ac 8 斜めに置かれた三角形の面積公式 b abc=l×h× 1 2 9 台形上の上底と下底に平行な線分の長さ b pq= × × 10 中線定理 d ab2ac2=2(am2bm2) 11 内接円を利用した三角形の面積 b 三角函數的基本定義 圖一 三角函數最一開始是用來表示角度和直角三角形三邊邊長關係的式子,直角三角形中的 sin x {\displaystyle \sin x} 和 cos x {\displaystyle \cos x} 可由畢氏定理給出它的定義: 若一個直角三角形,它的一個銳角角度為 x {\displaystyle x} ,此



初中三角函数公式图解 图片欣赏中心 急不急图文 Jpjww Com



1
検索語:三角比 三角関数の加法定理 三角比の三角形への応用 オイラー線の傾き 1 はじめに 高校数学「数学i」において三角比および三 角形などへの応用について学習する。応用の内 容は大体,正弦定理,余弦定理,三角形の解法,三角関数表(2) 角 正弦(sin) 余弦(cos) 正接(tan) 450 455 460 465 064 47他の三角比の計算ができることや、90 °までの三角比の表を用いて鈍角の三角比が求め られることを理解させる。 イ 三角比と図形 (ア)正弦定理、余弦定理 三角形abc のそれぞれの辺と角との間に懪り立つ基本的な関係として、 正弦定理 = =




求组合数取模 杨辉三角打表 求逆元 扩展欧几里得 费马小定理 欧拉定理 线性求法 Lucas 富士山下 程序员宅基地



高中三角函数公式表 高中三角函数公式表免费 七月seo
立体の体積、表面積 問題 ・・・ (む) は難しい問題です。 1 右図の四角錐の底面は1辺の長さ6 (cm)の正方形,側面は等しい辺の長さが2√7 (cm)の二等辺三角形です。 この四角錐の体積は (cm 3 ) ア= イ= この四角錐の表面積は (cm2) ウ= エ= オ= 2 右図は1辺の




这张初中数学公式表来得太及时了 初一到初三都能用 人人焦点




0到360度三角函數值表 特殊角的三角函數值表 每日頭條




三角函數微分表微積分公式復習表 Lvai



锐角三角函数公式大全 信息评鉴中心 酷米资讯 Kumizx Com



1



三角函数公式表




数学 三角比 Sin Cos Tanの表と覚え方 理系ラボ



三角函数公式表 亿帮常识网



三角函数公式表格图片 信息图文欣赏 信息村 K0w0m Com



三角函数值图像特殊三角函数值表的图 尚书坊




三角比の表と面積公式 正弦定理 余弦定理を一記事で解説




三角函数公式大全表格特殊值二倍角公式推导 计算机器在线计算



22 2 2相似三角形判定定理1表格式 图片欣赏中心 急不急图文 Jpjww Com



这张初中数学公式表来得太及时了 初一到初三都能用 速收藏 爱子网




初中三角函数公式表格 初中三角函数公式表 三人行教育网 Www 3rxing Org



1



高中三角函数公式表高中三角函数公式表



17全国1卷 理科 试卷分析与 黄金预测卷 对比 复习指导 组合教育




三角函数 维基百科 自由的百科全书




初中数学直角三角函数公式表 星火网校




大学数学公式大学数学的基础公式有哪些



高中数学 Sincostan特殊角的三角函数值表图 知识点总结 组合教育



古巴比伦楔形文字泥板刻有最古老三角函数表 每日环球展览 Imuseum



三角函数角度对照表 图片信息欣赏 图客 Tukexw Com



三角函数角度对照表 图片信息欣赏 图客 Tukexw Com



初中直角三角函数公式 初中数学三角函数公式 七月seo




三角函数表 高中数学三角函数公式总表 52fmz购物网



勾股定理公式计算 万图壁纸网
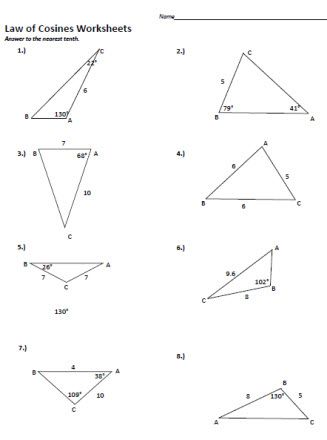



余弦定律对三角形图面积的影响




餘弦定理



来自高中数学三角函数公式总表 L 来自samm转学怎么并高中留级 高中课题目
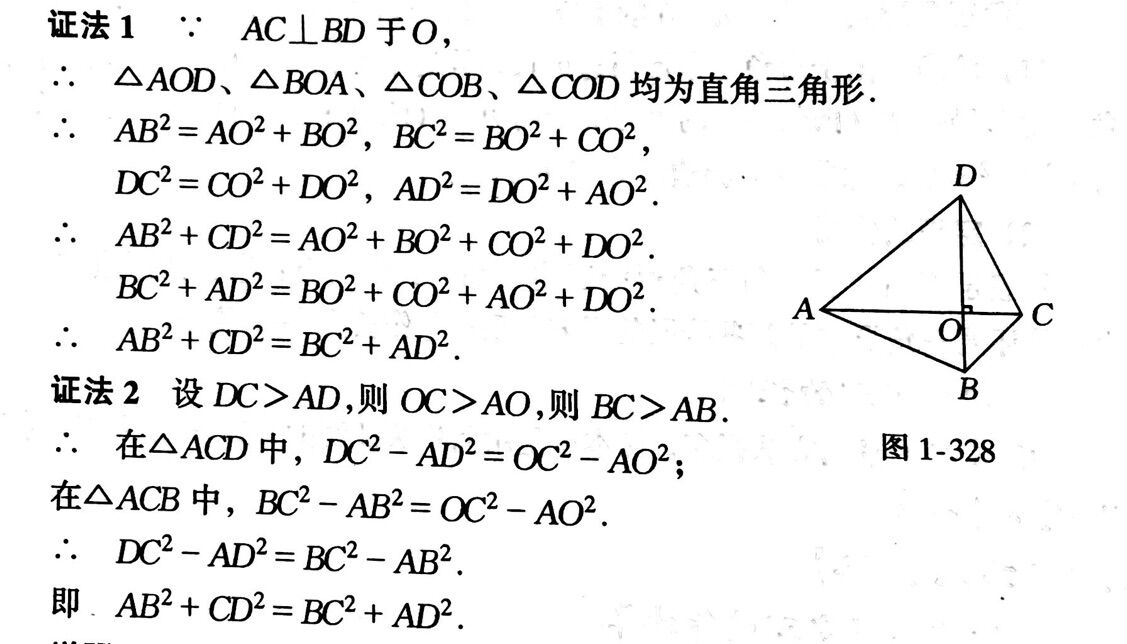



勾股定理及勾股定理的逆定理




三角函數表的來歷 每日頭條



反三角函数值表图第1页 驾考预约大全



初中数学三角函数表 初三网
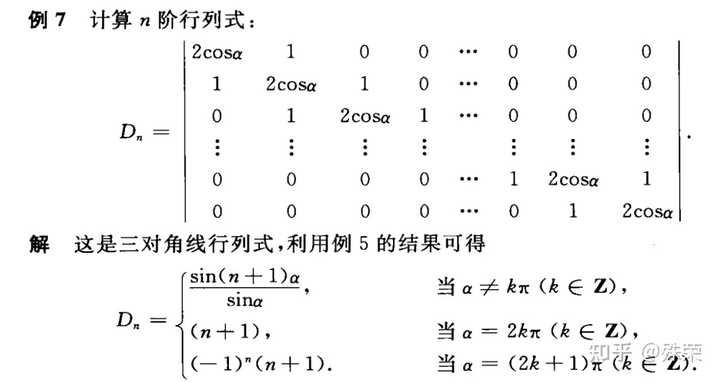



正切函数公式 三角函数公式 三角函数公式大全表格




三角函數微分積分表微積分2 5 Mrsysy



三角形勾股定理公式表勾股定理的所有公式勾股定理常用11个公式 我有车



三角函数公式表 亿帮常识网




三角函数值对照表 特殊角度的三角函数值 星火网校



三角函数值对照表 图片欣赏中心 急不急图文 Jpjww Com
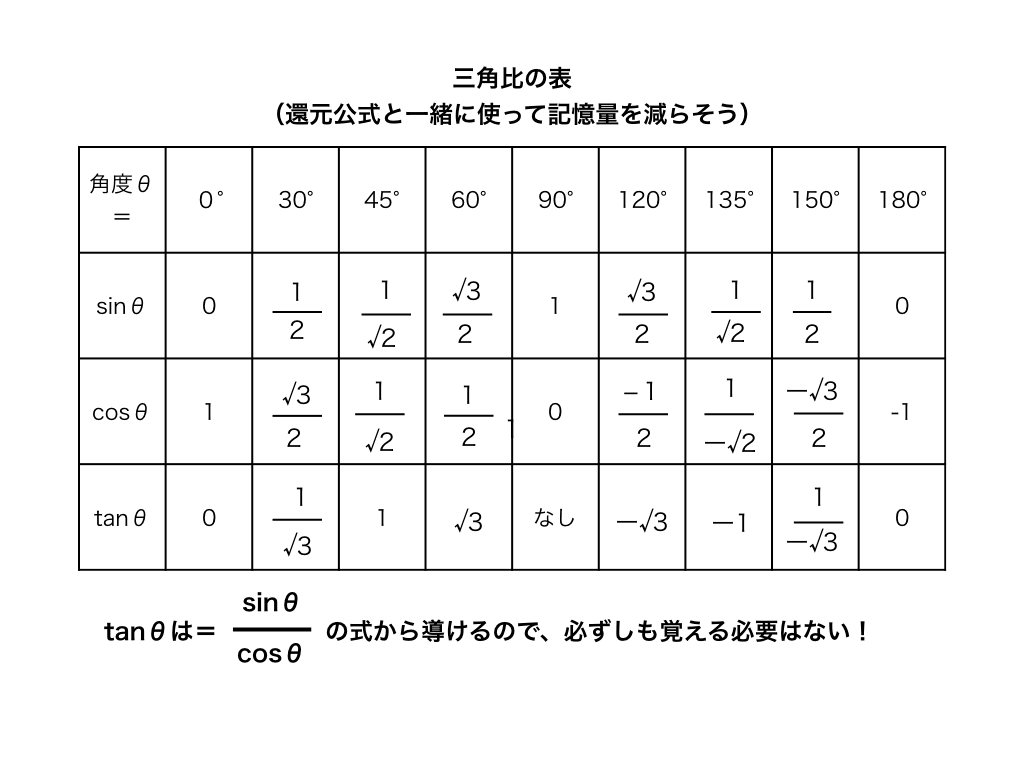



物理三角比




三角函数



中考数学知识点总结之三角函数公式表 平凉中考数学 精品学习网



1 3 2 杨辉三角 与二项式系数的性教案 教学设计



三角形勾股定理公式表勾股定理的所有公式勾股定理常用11个公式 我有车




三角函數微分表微積分公式復習表 Lvai



0到90的特殊三角函数值的变化 信息图文欣赏 信息村 K0w0m Com



初中勾股定理的证明方法中考 初中几何题证明思路总结 教案网



探索勾股定理 勾股定理ppt 第1课时 第一ppt



反三角函数值表特殊三角函数值表 学习岛




Cos 公式三角函數cos公式表 高三網 Nqnpg



三角函数公式表格图片 信息评鉴中心 酷米资讯 Kumizx Com



1




三角函数表值对照表 三角函数公式大全表格 三角函数表值查表
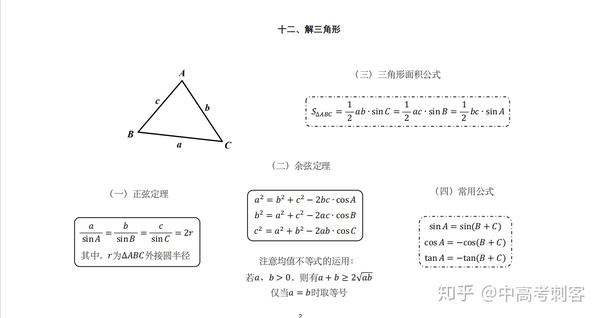



高中数学三角函数表 衡水中学归纳整理 干净利索 常用三角函数表格 东煤网




直角三角形面积公式表怎么算计算公式方法详解 小街网




大学数学公式大学数学的基础公式有哪些



初三数学三角函数 三角函数公式大全表格 函数查询




三角函式對數表 三角函式對數表是一種常用的數據表 指具有一定間隔的銳角三 百科知識中文網




三角学 维基百科 自由的百科全书



最全三角函数公式推导 知乎



初中三角函数 三角函数公式大全 三角函数公式 007鞋网



三角函数值大全表图 万图壁纸网



反三角函数值表特殊三角函数值表 学习岛



古巴比伦楔形文字泥板刻有最古老三角函数表 每日环球展览




超全的0到360度三角函數值表 以及特殊角的三角函數值表 壹讀



正切函数表三角函数值 三角函数表值查表



三角形勾股定理公式表勾股定理的所有公式勾股定理常用11个公式 我有车



勾股定理及其逆定理 初中数学知识点 教育杏坛




三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学




Cos 公式三角函數cos公式表 高三網 Nqnpg



三角函数练习题相比起三角函数这款自主suv更容易让人记住 尚书坊



初一到初三都能用的公式表 赶紧收藏备用 小初高题库试卷课件教案网



三角函数公式及其定理 信息评鉴中心 酷米资讯 Kumizx Com



17 1 勾股定理 人教版八年级下册数学电子课本 数九网



反三角函数值表 万图壁纸网



三角函数公式表图初中三角函数公式表



22 2 2相似三角形判定定理1表格式 图片欣赏中心 急不急图文 Jpjww Com




銳角三角形面積常見的平面圖形周長 面積計算公式表 Qhcoh




数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ



正切函数表1一90度 万图壁纸网



这张初中数学公式表来得太及时了 很多初三的内容都会在初二进行学习 速收藏 初中 姜橙教育网



常用三角函数值口诀 初三网




三角函数表 高中数学三角函数公式总表 52fmz购物网



0到90的特殊三角函数值的变化 信息图文欣赏 信息村 K0w0m Com




常用三角函数 导数 极限pdf Pdf




锐角三角函数表是什么 常用三角函数值表 8啦



0 件のコメント:
コメントを投稿